|
移动无线信道是弥散信道。电波通过移动无线信道后,信号在时域上或在频域上都会产生弥散,本来分开的波形在时间上或在频谱上会产生交叠,使信号产生衰落失真。 |
式中入射角θ,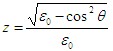 , (垂直极化) , (垂直极化)2、 两径传播模型 |
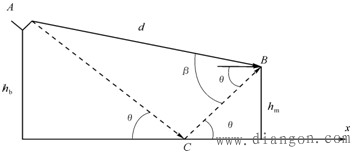 |
| 图1 两径传播模型 |
| 图1表示有一条直射波和一条反射波路径的两径传播模型。图1中,A表示发射天线;B表示接收天线;hb和hm分别表示发射天线和接收天线离地面的高度;AB表示直射波路径;ACB表示反射波路径。 在接收天线B处的接收信号功率表示为 |
| 在大多数场合,地表面波的影响可以忽略,则上式可以简化为 |
| 其中,相位差 |
| 3.多径传播模型 |
| 其中,N为路径数。当N很大时,无法用公式准确计算出接收信号的 功率,必须用统计的方法计算接收信号的功率 二、多普勒频谱 当移动体在x轴上以速度 v移动时引起多普勒(Doppler)频率漂移。用一个平面波表示稳定扩散事件,假定xOy平面是平面场,此时,多普勒效应引起的多普勒频移可表示为 |
| 当第n个入射波的入射角是 设发射信号是垂直极化,并且只考虑垂直波时,场强Ez可以表示为 |
 |
| 根据中心极限理论,当N很大时,近似为高斯随机过程,Ez可以表示为 |
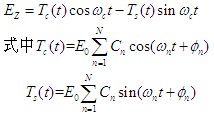 |
| 且Tc(t)、Ts(t)是高斯随机过程, Tc、Ts为随机变量。对应固定时间t, Tc、Ts有0平均和等方差 |
| 一个单频信号通过移动无线信道后,衰落信号的包络发生随机变化,其相位也会发生随机变化。 移动台的运动造成接收信号产生多普勒频移, 在多径传播环境中,对于接收机有不同时延的反射路径。每个路径产生相同的多普勒频移。 多普勒效应的结果是通过移动的多径信道后单频信号的频谱扩展为 若收到多条有不同入射角的多径信号,多普勒频移成为多普勒扩展频谱,称做多径衰落信号的随机调频。 多普勒扩展的倒数就是对信道相关时间的度量,即信道的相关时间 时间选择性衰落是由多普勒效应引起的,并且发生在传输波形的特定时间段上,即信道在时域具有选择性。 三、瑞利衰落分布和莱斯衰落分布 讨论多径信道的包络统计特性,接收信号的包络根据不同的无线环境一般服从瑞利分布和 莱斯分布 1、瑞利分布 环境条件: 通常在离基站较远、反射物较多的地区符合(如下图) |
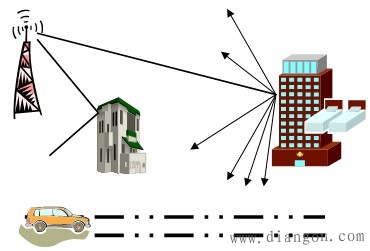 |
| (1)发射机和接收机之间没有直射波路径; (2)存在大量反射波,到达接收天线的方向角随机且0~2π均匀分布 (3)各反射波的幅度和相位都统计独立 推导过程如下: 设发射信号是垂直极化,并且只考虑垂直波时,场强为 其中 Tc,Ts的性质: (1)相互正交的同频分量 (2)高斯随机过程概率密度 (3)统计独立联合概率密度 |
(4)零均值,等方差,不相关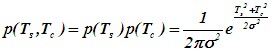 < >是关于x = Tc或Ts 的总体平均 |
| 接收信号的幅度分布 直角坐标→极坐标 则由雅各比行列式 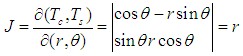 所以 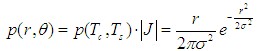 对 r 积分 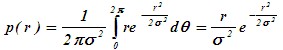 对θ积分 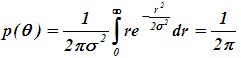 可见,包络 r 服从瑞利分布,θ在0~2π内服从均匀分布 |
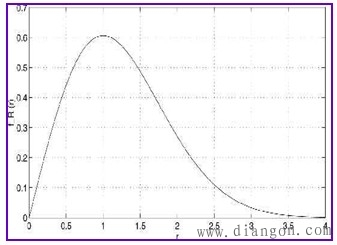 |
| 图3 瑞利分布的概率分布密度 |
| 瑞利分布的均值 瑞利分布的方差 满足 |
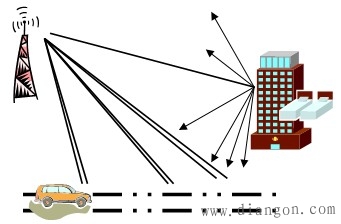
| 2、莱斯分布 莱斯分布的环境条件: (1)直射系统中,接收信号中有视距信号成为主导分量,同时还有不同角度随机到达的多径分量迭加于其上。如下图所示。 (2)非直射系统中,源自某一个散射体路径的信号功率特别强。 |
 |
| 莱斯分布的概率密度函数 概率密度函数 |
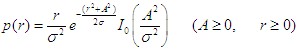 |
| 式中, A是主信号的峰值 I0(·)是0阶第一类修正贝塞尔函数 莱斯因子K 主信号的功率与多径分量方差之比 |
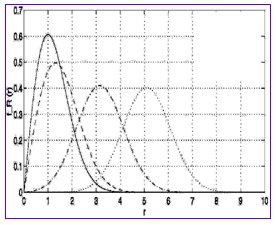 |
| 图4 莱斯分布的概率密度函数 |
| 分贝式 意义: (1)当 (2)强直射波的存在使接收信号包络从瑞利变为莱斯分布 (3)当直射波进一步增强( 3.4.4 时延扩展 图3.9中,描述多径时延谱的参数有 (1)p(τ)为归一化时延信号的包络,近似为指数曲线。 |
| (2)Tm为最大时延扩展,归一化时延信号包络p(τ)=-XdB时所对应的时延差值。 (3)τa为归一化时延谱曲线的数学期望(平均延时) |
| (4)Δ为归一化时延谱曲线的均方值时延扩展 |
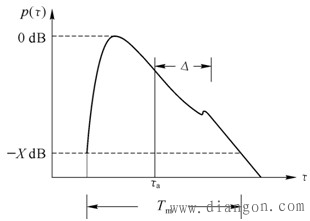 |
| 图5 典型的归一化时延谱图 |
| 四、时延扩展 均方根时延扩展Δ是对多径信道时延特性的统计描述,其含义表示时延谱扩展的程度。Δ值越小,时延扩展就越轻微;反之,时延扩展就越严重,表征时延扩展对平均延时τa的偏离程度。 在数字传输系统中,由于时延扩展,接收信号中一个码元的波形会扩展到其他码元周期中,引起码间串扰。为避免码间串扰,应使码元周期大于时延扩展。不同环境下平均时延扩展是不一样的 五、相关带宽 首先考虑图6所示的两条路径信道模型情况。第一条路径信号为Si(t),第二条路径信号为 两路径信道的等效网络传递函数为 |
| 信道的幅频特性 |
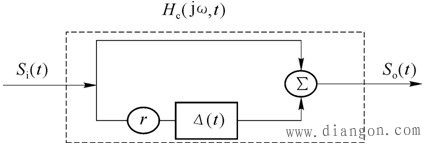 |
| 图6两条路径信道模型 |
| 1、相关带宽 设两个信号的包络为 |
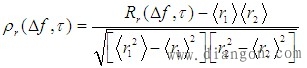 |
此处,相关函数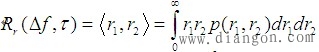 若信号衰落符合瑞利分布,则 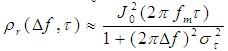 式中, 不失一般性,可令 |
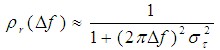 |
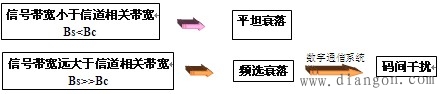
| 通常,根据包络的相关系数 相关带宽 2、衰落的分类 |
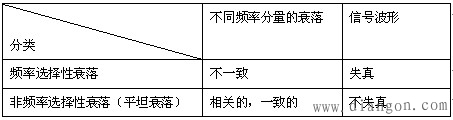 |
| 3、衰落的判定 由信道和信号两方面决定 |
 |
| 六、衰落特性 通常用衰落深度、衰落速率、衰落持续时间、电平通过率等特征量来描述信道的衰落特性。 1、电平通过率:单位时间内信号包络以正斜率通过某一规定电平值R的平均次数。 2、平均衰落持续时间:信号包络低于某个给定电平值的概率与该电平所对应的电平通过率之比。 |
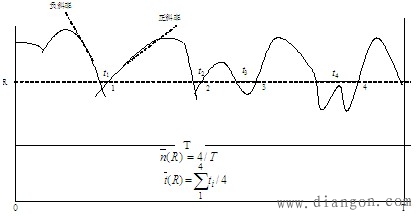 |
| 图7电平通过率与平均衰落持续时间 |
| 电平通过率 |
 |
| 平均衰落持续时间: |
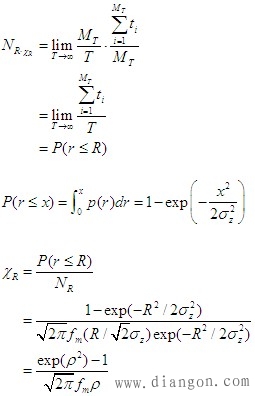 |
| 知道平均衰落持续时间可确定在一次衰落期间丢失的比特数 |
电工学习网 ( )
GMT+8, 2021-12-6 20:45