| 本文研究的问题是信道中存在加性高斯白噪声时，各种线性调制系统的抗噪声性能。考虑到信道中加性噪声只对已调信号的接收产生影响，因而调制系统的抗噪声性能可用解调器的抗噪声性能来衡量。分析模型如图1所示。 |
 |
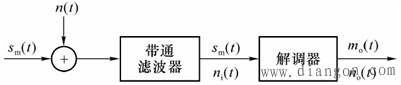| 图1 解调器的抗噪声模型 |
图中， 为已调信号（如AM、DSB、SSB、VSB）； 为信道加性噪声，是均值为零的高斯白噪声；带通滤波器的作用滤除已调信号频带以外的噪声，因此解调器输入端的信号仍为 ，噪声变为窄带高斯噪声 ，表示式为 |
 |
且 （均值） |
 （平均功率） |
式中，B是理想带通滤波器的带宽，即为已调信号的带宽，也是解调器输入噪声的带宽； 是噪声单边功率谱密度； 是解调器的输入噪声功率。解调器可以是相干解调器和非相干解调器。相干解调属于线性解调，故在解调过程中输入信号和噪声可以分开解调；非相干解调属于非线性解调，信号与噪声无法分开解调。 评价模拟通信系统的质量性能指标可用输出信噪比 |
 |
| 也可用调制制度增益（解调增益） |
 |
其中， 为解调器的输入信噪比，定义为 |
 |
显然，输出信噪比不仅与调制方式有关也与解调方式有关。在相同的 和的条件下，输出信噪比越高，解调器的抗噪声性能越好。一、DSB系统的抗噪声性能 DSB信号采用相干解调时的模型。 |
 |
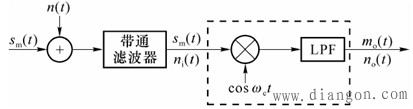| 图2 DSB相干解调抗噪声性能分析模型 |
| 解调器输入信号为 |
 |
| 解调器输出信号为 |
 |
| 解调器最终输出噪声为 |
 |
| 输入信号的平均功率 |
 |
| 解调器输入噪声的平均功率 |
 |
其中 ，为双边带信号的带宽。解调器的输入信噪比 |
 |
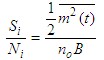| 解调器输出信号功率 |
 |
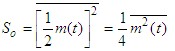| 解调器输出噪声功率 |
 |
| 解调器输出信噪比 |
 |
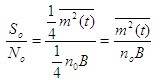| 调制制度增益为 |
 |
由此可见，对于DSB调制系统而言，调制制度增益为2。这就是说，DSB信号的解调器使信噪比改善一倍。这是因为采用相干解调把噪声中的正交分量 抑制掉的缘故。二、SSB系统的抗噪声性能 分析模型与DSB相干解调器相同。在抗不同之处在于带通滤波器的带宽是DSB的一半。 解调器输入端输入单边带信号为 |
 |
| 解调器输入端信号功率为 |
 |
| 解调器输入噪声功率 |
 |
其中 ，为单边带信号的带宽。单边带解调器输入信噪比为 |
 |
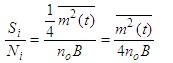| 解调器输出信号为 |
 |
| 解调器输出端信号功率为 |
 |
| 解调器输出端噪声功率 |
 |
| 单边带解调器输出端信噪比为 |
 |
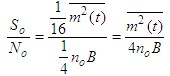| 调制制度增益为 |
 |
| 三、AM系统的抗噪声性能 AM信号既可以采用相干解调也可以采用非相干解调，不同的解调方式抗噪声性能是不同的。由于AM信号采用非相干解调方式较多，在此介绍采用包络检波器解调AM信号的抗噪声性能。此时，图1所示模型中的解调器为包络解调器，如图3所示。 解调器输入信号为 |
 |
 |
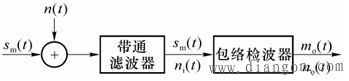| 图3 AM信号包络检波的抗噪声性能分析模型 |
| 输入信号功率为 |
 |
| 输入噪声为 |
 |
| 输入噪声功率为 |
 |
其中 输入信噪比为 |
 |
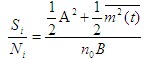为了求出包络检波器输出端信噪比，亦即求出包络检波器输出端信号功率 和噪声功率 ，有必要求检波器输入端信号和噪声的混合信号的包络。包络检波器输出端的信号正比于检波器输入混合信号的包络。 |
 |
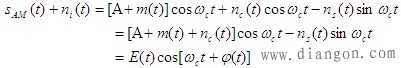| 其中 |
 |
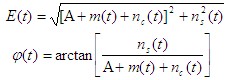很明显， 便是所求的混合信号的包络， 是混合信号的相位。理想包络检波器的输出就是。1．大信噪比情况 所谓大信噪比是指满足下列条件，即 |
 |
| 于是式可写为 |
 |
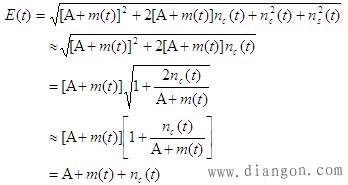| 可见，包络检波器输出信号为 |
 |
| 输出信号功率为 |
 |
| 输出噪声为 |
 |
| 输出的噪声功率为 |
 |
| AM解调器输出信噪比为 |
 |
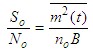| AM系统调制制度增益 |
 |
对于100%调制（即 ），且 为正弦波时，有 |
 |
| 需要指出，若采用相干解调法解调AM信号，得到的调制制度增益G与包络检波时的相同。由此可见，对于AM调制系统，在大信噪比时，采用包络检波器与相干解调器解调性能几乎一样。 2．小信噪比情况 所谓小信噪比是指满足下列条件，即 |
 |
| 在小信噪比情况下，信号无法与噪声分开，而且由于信号“淹没”在噪声中，这时输出信噪比不是按比例随输入信噪比下降，而是急剧恶化。这种现象通常称为“门限效应”。开始出现门限效应的输入信噪比称为“门限”。 相干解调不存在门限效应。原因是信号与噪声分别解调，故解调器输出端总是单独存在有用信号项。 |
匹配滤波接收机
最佳接收准则
影响信号可靠传输的主要因素
多进制数字调制系统
各种二进制数字调制系统的比较
二进制绝对相移键控（2PSK）与相对相移键控电工学习网 ( )
GMT+8, 2021-12-6 20:45
