|
平稳随机过程的是一种特殊而又广泛应用的随机过程。 一、平稳随机过程定义 1.狭义平稳 定义 随机过程  的 维分布函数或维概率密度函数与时间起点无关，即对于任何和 ，随机过程的维概率密度函数满足 |
 |
| 则称是在严格意义下的平稳随机过程。简称严平稳随机过程或狭义平稳随机过程。 平稳随机过程的统计特性将不随时间的推移而不同。它的一维概率密度函数与时间  无关，即 |
 |
| 而二维概率密度函数仅依赖于时间间隔 有关，即 |
 |
| 2.广义平稳 定义： 若随机过程 的数学期望及方差与时间无关，而自相关函数仅与时间间隔有关，即 |
 |
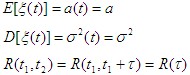| 则称为广义平稳随机过程或宽平稳随机过程。 通信系统中所遇到的信号及噪声大多数可视为广义平稳随机过程。以后讨论平稳随机过程除特殊说明外均指广义平稳随机过程。 二、各态历经性 各态历经性是平稳随机过程在满足一定条件下的一个非常重要的特性。 设  是平稳随机过程中任取的一个样本函数，若的数字特征（统计平均）可由的时间平均值替代，即 |
 |
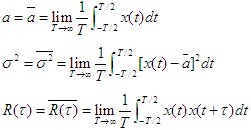| 则称随机过程具有各态历经性。 “各态历经”的含义：从随机过程中得到的任何一个样本函数，都经历了随机过程的所有可能状态。因此，可用一个样本函数得统计特性来了解整个过程的统计特性，从而使“统计平均”化为“时间平均”，使实际测量和计算的问题大为简化。 注意：只有平稳随机过程才可能具有各态历经性，但在通信系统中所遇到的随机信号和噪声，一般均能满足各态历经性条件。 三、平稳随机过程的相关函数与功率谱密度 1.平稳随机过程自相关函数的性质 平稳随机过程自相关函数的定义式 |
 |
| 性质： （1）  （的平均功率） （2）  （ 是偶函数）（3）  （ 时有最大值，为上界值）（4）  （的直流功率） （5）  （方差，为的交流功率） |
| 由上述性质可知，用自相关函数可表述的几乎所有的数字特征，因而具有实用意义。 例3.3.1 设随机过程  ，其中 是在 内均匀分布的随机变量。试证明：（1） 是广义平稳的；（2）试说明它的自相关函数的性质。证明：(1)按题意，随机相位 的概率密度函数为 |
 |
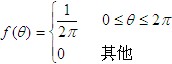| 则的数学期望为 |
 |
| 的自相关函数为 |
 |
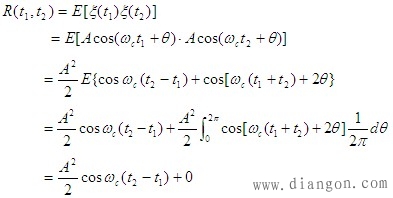令 ，得 。可见的数学期望为常数（等于0）而自相关函数只与时间间隔有关，所以为广义平稳随机过程。(2) 画出它的自相关函数 的曲线图3.3.1。由图可见， 为的偶函数； ，其直流功率经计算得 ，说明无直流功率，这时交流功率就是 。 |
 |
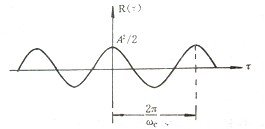| 图3.3.1 随机相位余弦波的自相关函数 |
| 2. 平稳随机过程的功率谱密度 对于任意的确定功率信号  ，它的功率谱密度 可以表示成 |
 |
式中 是的截短函数 的频谱函数。平稳随机过程的每个实现（样本函数）是一个时间信号，且为功率信号，因而每个实现的功率谱密度可由上式表示。但是随机过程的每一个实现是不能预知的，因此，某一实现的功率谱密度不能当作平稳随机过程的功率谱密度，而必须进行统计平均。 与确定功率信号相似，令  是随机过程的某一实现的截短函数，且其傅里叶变换存在，即有 。可以得到平稳随机过程的功率谱密度 为 |
 |
| 而的平均功率为 |
 |
| 随机过程功率谱密度的性质： （1）  非负性（2）  实偶性 |
| 3.功率谱密度与自相关函数的关系 维纳-辛钦关系 |
 |
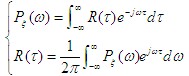| 简记为 |
 |
| 的自相关函数和功率谱密度是一对傅里叶变换。 在维纳-辛钦关系的基础上，我们可以得到如下结论： (1)对功率谱密度进行积分，可以得到平稳随机过程的总功率。 |
 |
这正是维纳-辛钦关系的意义所在，它不仅指出了用自相关函数来表示功率谱密度，同时还从频域的角度给出了随机过程平均功率的计算方法，而式 是时域的计算方法。例3.3.2 求随机相位余弦波  的自相关函数和功率谱密度。解：在例3.3.1中，我们已经得出 是广义平稳的随机过程，并且求出其自相关函数为 |
 |
根据维纳-辛钦关系，即 ，由于 |
 |
| 所以，功率谱密度为 |
 |
| 而平均功率为 |
|
匹配滤波接收机
最佳接收准则
影响信号可靠传输的主要因素
多进制数字调制系统
各种二进制数字调制系统的比较
二进制绝对相移键控（2PSK）与相对相移键控电工学习网 ( )
GMT+8, 2021-12-6 20:45
