|
虽然用随机过程的 维分布函数或 维概率密度函数能够完善地描述随机过程 |
 |
并记为 ， 是一时间函数，它表示随机过程各个时刻的数学期望随时间的变化情况，其本质就是随机过程所有样本函数的统计平均函数。图3.2.1画出了随机过程 的 个样本函数 和它的数学期望。 |
 |
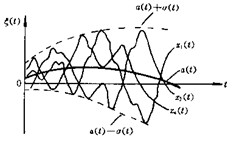| 图3.2.1 随机过程的数学期望和方差 |
| 二、方差 定义： |
 |
| 由此可得 |
 |
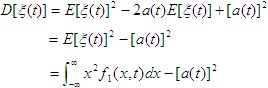 也常记作 ,它表示随机过程在时刻 对于均值的偏离程度，见图3.2.1。 称为随机过程均方差。当均值  时，方差为 三、自协方差函数和自相关函数 数学期望 和方差描述了随机过程在各个孤立时刻的特征，但没有反映随机过程不同时刻之间的内在联系。自协方差函数 和自相关函数 就是用来衡量随机过程在任意两个时刻上获得的随机变量的统计相关特性的。1.自协方差函数 定义 |
 |
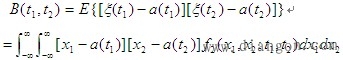其中， 与 为两个任意时刻； 与 为在和上所得到的数学期望； 为二维概率密度函数。2.自相关函数 定义 |
 |
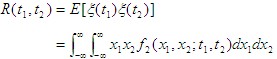| 二者关系： |
 |
| 上面的和是衡量同一个随机过程的相关程度的。 四、互协方差和互相关函数 如果把自相关函数的概念引伸到两个或多个随机过程中，可以得互协方差或互相关函数。设 和 分别表示两个随机过程，则1.互协方差函数 定义 |
 |
| 2.互相关函数 定义 |
 |
由以上分析可见，随机过程的统计特性一般都与时刻 有关。就相关函数而言，它的相关程度与选择时刻及有关。如果 ，可令 ，则自相关函数 可以表示为 ，这说明，相关函数依赖于起始时刻及时间间隔 ，即相关函数是和的函数。
|
匹配滤波接收机
最佳接收准则
影响信号可靠传输的主要因素
多进制数字调制系统
各种二进制数字调制系统的比较
二进制绝对相移键控（2PSK）与相对相移键控电工学习网 ( )
GMT+8, 2021-12-6 20:45
