|
一、随机过程的基本概念 随机过程的定义 当事物的变化的过程不能用一个或几个时间的确定函数来描述时，则称这个过程为随机过程。 |
 |
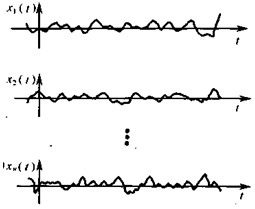图1  部通信机的噪声输出记录 |
| 这种过程的基本特征是：其一，在观察区间内是一个时间函数；其二，在任意时刻上观察到的值是不确定的，是一个随机变量。 随机过程可以定义为赖时间参数 变化的随机变量的总体或集合。 随机过程中每个时间函数称为一个样本函数，随机过程就可以看成是一个有全部可能的样本函数构成的总体，即样本函数的总体或集合，记为  。随机过程有两个基本属性： （1） 是一个时间函数；（2）给定任意一个时刻  ， 是一个不含 变化的随机变量。二、随机过程的一般描述 设 是一个随机过程，则它在任意一个时刻的值是一个随机变量。而随机变量的统计特性是可以用概率分布函数或概率密度函数来描述的。我们把 的概率 记作 ，称为随机过程的一维分布函数，即 |
 |
设上式对 的偏导数存在，这时随机过程的一维概率密度函数可定义为 |
 |
| 显然，随机过程的一维分布函数和一维概率密度函数仅仅描述了随机过程在各个孤立时刻的统计特性，而没有反映随机过程在各个时刻取值之间的内在联系。因此，还需要在足够多的时刻上考虑随机过程的多维分布函数。 随机过程 的维概率分布函数被定义为 |
 |
| 的维概率密度函数（如果存在） |
 |
| 显然，越大，用维分布函数或维概率密度函数描述随机过程的统计特性就越充分。
|
匹配滤波接收机
最佳接收准则
影响信号可靠传输的主要因素
多进制数字调制系统
各种二进制数字调制系统的比较
二进制绝对相移键控（2PSK）与相对相移键控电工学习网 ( )
GMT+8, 2021-12-6 20:45
