|
单模光纤的研制和应用之所以越来越深入,越来越广泛,这是由于单模光纤不存在模式色散,因而其总色散很小,即带宽很宽,能够传输的信息容量极大,加之石英光纤在1.31 μm和1.55 μm波长窗口附近损耗很小,使其成为长途大容量信息传输的理想介质.、因此如何选择单模光纤的设计参数,特别是其色散特性参数,一直是人们所感兴趣的一个具有实际意义的研究课题. 1.产生色散现象的原因 从前面的分析可知,光纤自身存在色散,即材料色散、波导色散和模式色散.对于单模光纤,因为仅存在一个传输模,故单模光纤的色散只包括材料色散和波导色散.除此之外,还存在着与光纤色散有关的种种因素,会使系统性能参数出现恶化,如误码率、衰减常数变坏.其中比较重要的有三类:码间干扰、模分配噪声、啁啾声。 在此,重点讨论由这三种原因造成的对系统中继距离的限制. 2.码间干扰对中继传输距离的影响 由众所周知的原因,当光脉冲信号通过一段光缆后,或多或少会使传输信号发生畸变, 即脉冲展宽,严重时造成码间干扰,影响数字系统中的码判决,因此码间干扰一直是人们关注的问题之一. (1)码间干扰的概念 由于激光器所发出的光波是由许多根线谱构成的,而每根线谱产生的相同波形在光纤中传输时,其传播速度不同,使得所经历的色散不同,而前后错开,使合成的波形不同于单根线谱的波形,导致所传输的光脉冲的宽度展宽,出现“拖尾”,因而造成相邻两光脉冲之间的相互干扰,这种现象称为码间干扰. (2)码间干扰对中继距离的影响 归根到底码间干扰是由于信号通过光信道产生色散引起的,因此,首先分析一下光纤传输函数.由此拢出中继距离与输入、输出光脉冲之间的关系. ①光纤的传输函数 一段光纤的传输特性,可以用一个二端口网络来等效,如图4-28所示.图中Pin(t)和Pout(t)分别为输入、输出端光脉冲的波形函数;Pin(ω)和Pout(ω)分别为对应的输入、输出端光脉冲的频谱函数, |
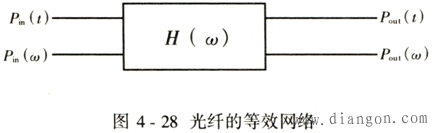 |
| 那么该网络频率特性可以用下式确定 |
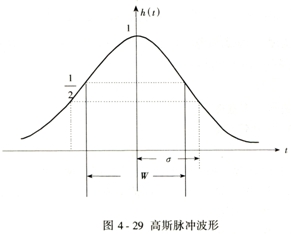
| 式中,称为网络的频率传输函数。若设输入、输出的光脉冲均为高斯脉冲波形,如图4-29所示,即输入、输出光脉冲分别为 |
| 式中,σ1——输入脉冲均方根宽度的一半; σ2——输出光脉冲均方根宽度的一半; TD——光纤的时延。 |
 |
| 根据频谱函数的定义,输入、输出波形的傅里叶积分便为其频谱函数,那么 |
| 同理 |
| 将上述结果代入式(4-9)中,得到光纤的传输函数为 |
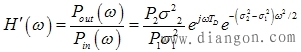 |
|
对上式进行观察,可以发现其分式 |
| 其中, |
| 再令H(ω)=1/2,代入上式,可求得半功率点处相应的截止角频率ω0(截止频率f0),其结果为 |
| 若将上式代人式(4-13)中,则 |
 |
| 至此,就得到了以截止频率为参量的光纤传输函数. ②由光信道引入的展宽脉冲的均方根σ和半功率点宽度W 由式(4-14)可知,由于光纤色散的作用,使所传输的光信号出现脉冲展宽的现象,因而输出光脉冲的均方根σ2比输入光信号的均方根σ1大,而σ则代表展宽光脉冲的均方根值,那么如果光纤的色散愈严重,则展宽光脉冲的均方根值σ愈大. 当然式(4-15)也可以被认为是一个δ脉冲经过特性为H(f)的网络后,其输出波形的表示式.由于δ脉冲的宽度是趋近于零的,所以上述波形的宽度即为脉冲波形通过光纤后的脉冲展宽值.若与高斯波形比较,可以看出,δ脉冲的输出波形,仍是一个高斯形状,在实际中,常用最大高度一半的宽度W来衡量脉冲展宽的严重程度,即 |
| 由于式(4-14)戍立,因而可以导出: |
| 其中,W1为输入脉冲的半功率宽度; W2为输出脉冲的半功率宽度. ③带宽与长度的关系 如上所述,光纤带宽由其截止频率决定,而光纤的截止频率的大小与脉冲展宽的均方根值σ成反比.当光纤越长时,脉冲展宽的均方根值σ越大,由此可知,光纤的带宽与光纤的长度有关,但不一定与长度L成反比. 如果l km光纤的3 dB带宽为Bc(MHz·km),则长度为L(km)的光纤的全程光纤带宽B为 |
| 上式严格地讲是对应于由于模式色散引起的带宽值.其中γ称为带宽长度系数,对多模光纤来讲,光脉冲在光纤中传播时会产生模式变换,因而模间色散得以减轻,故其有效长度要减小,一般取γ为0.5~0.9.对单模光纤而言,因无模间色散,故取γ为l,即 |
| 或 |
| ④光纤带宽与半功率点宽度W之间的关系 根据信号系统的知识和式(4-15)可知,光纤等效网络的冲击响应为 |
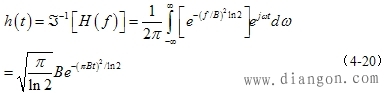 |
| 另外,根据前面W的定义可知, |
| 那么半功率点宽度W为 |
| 式(4-22)表示波形展宽的半功率点宽度W与光纤3 dB带宽B之间的关系,它为工程中的换算带来很大的方便, ⑤码间干扰对中继距离的限制 较大的脉冲展宽会发生严重的码间干扰,使误码率增加,限制了传输距离.在进行系统设计时,一般采用相对均方根脉宽α,其数值上等于光脉冲均方根宽度的一半与光脉冲周期的比值,即α=σ/T,在工程中通常取α≤0. 35.若此时光纤上所传输的码速率为fb,或周期为T,并且假设可以忽略光纤的材料色散,或者可以近似地归入脉冲展宽σ内,则对于均方根为σ1的半占空比脉冲,经光纤传输之后,在输出端接收到的输出光脉冲如图4-30所示,根据式(4-14),可得光纤输出的脉冲半功率点宽度W2近似为 |
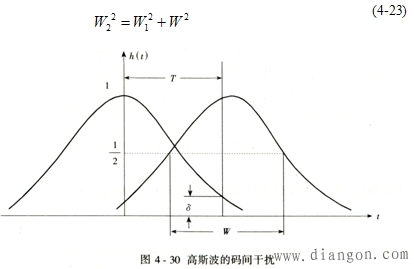 |
| 其中,W1为输入脉冲的半功率宽度。对于一个周期为T的标准矩形脉冲来说,W1=T/2; W为δ信号经光纤传输后的脉冲宽度值,由式(4-22)决定。 因此式(4-23)可以改写成 |
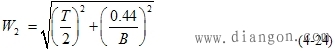 |
| 对于高斯波形而言,其输出光脉冲均方根脉宽σ2与半功率点宽度W2之间的关系为 |
| 又因为相对均方根脉宽 |
| 若以上式代入式(4-24)中,便可求得所需的全程光纤带宽 |
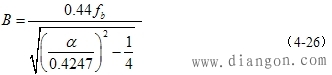 |
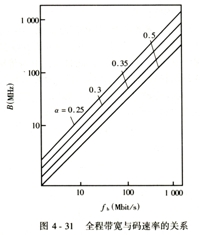
| 这样,便找出了传输速率fb与光纤带宽之间的关系,并绘与图4-31中。有图可知,系统的传输速率越高,对系统所要求的传输带宽越宽。 |
 |
| 如果已知长度为L的单模光纤的全程带宽为B,则由式(4-17)可求得1 km光纤的带宽为 |
| 由式(4-22),(4-26),(4-27)可求得光纤带宽所限制的传输距离为 |
 |
| 其中,W是1 km光纤的脉冲展宽量。 如果根据色散定义,可知1 km光纤的脉冲展宽W=D(λ)δλ,因此式(4-28)又可以改写成 |
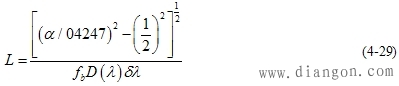 |
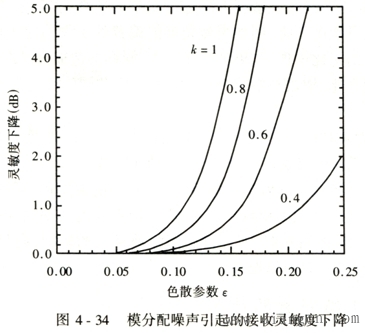
| 根据具体情况选取适当的α值(0.3~0.35)代人,可见式(4-29)的分子为一常数,而传输距离与码速、光纤的色散系数以及光源谱宽成反比,即系统的传输速率愈高,光纤的色散系数愈大,光源谱宽愈宽.为了保证一定传输质量,系统所能传输的中继距离愈短. 从以上分析可以看出,式(4-29)是对输入光脉冲呈现高斯分布的假设下得到的中继距离公式,当然采用其他形式的数学模型来模拟会得到不同形式的中继距离表达式,因此目前对中继距离的理论分析表达式有若干种,但其变化趋势是一致的,都能够反映光纤的传输特性,对实际工作有一定的指导意义. 3.模分配噪声对中继距离的影响 如果数字系统的码速率尚不是超高速,并且单模光纤的色散可忽略的情况下,不会发生模分配噪声,但随着技术的不断发展,更进一步地充分发挥单模光纤大容量的特点,提高传输码速率越来越提到议事日程,随之人们要面对的问题便是模分配噪声了。 由于在高速率下激光器的谱线和单模光纤的色散相互作用,产生了一种叫模分配噪声的现象,它限制了通信距离和容量,但为什么激光器的谱线和单模光纤的色散相互结合会产生模分配噪声呢?要回答这一问题,首先要从激光器的谱线特性谈起. (l)激光器的谱线特性 当普通激光器工作在直流或低码速情况下,它具有良好的单纵模(单频)谱线,如图4-32(a)所示,这样当此单纵模耦合到单模光纤中之后,便会激发出传输模,从而完成信号的传输.然而在高码速(如565 Mbit/s)情况下,其谱线呈现多纵模(多频)谱线,如图4-32(b)所示.而且从图4-33可以看出,各谱线功率的总和是一定的,但每根谱线的功率是随机的,换句话讲,即各谱线的能量随机分配.可想而知,由这样多个能量随机分配的谱线,在光纤中各自激励其传输模之后会形成何等局面. (2)模分配噪声的产生 因为单模光纤具有色散,所以激光器的各谱线(各频率分量)经过长光纤传输之后,产生不同的迟延,在接收端造成了脉冲展宽,又因为各谱线的功率呈随机分布,因此当它们经过上述光纤传输后,在接收端取样点得到的取样信号就会有强度起伏,引入了附加噪声,这种噪卢就称为模分配噪声.由此还看出,模分配噪声是在发送端的光源和传输介质光纤中形成的噪声,而不是接收端产生的噪声,故在接收端是无法消除或减弱的. 这样当随机变化的模分配噪声叠加在传输信号上时,会使之发生畸变,严重时,使判决出现困难,造成误码,从而限制了传输距离. (3)模分配噪声对灵敏度的影响 据资料分析显示,在使用多纵模半导体激光器的系统中,由其多纵模的起伏性和光纤色散而引起的灵敏度下降如图4-34所示,其中k为模分配系数,一般k的值在o~1之间,对于不同的激光器而言其k值不同,而且实际上不同模式之间,k值也不同,在图4.34中给出了BER=10-9情况下,不同模分配系数k条件下,灵敏度下降随色散代价有关参数ε的关系. 从图中可以看出,在给定的k值情况下,如当ε<0.1时,由模分配噪声引起的灵敏度下降可以忽略(小于0.5dB),但随着ε的增加,灵敏度下降增加很快,同时在k>0.5时,在相同的ε值下,模分配噪声引起的灵敏度下降大于色散导致的脉冲展宽引起的灵敏度下降. |
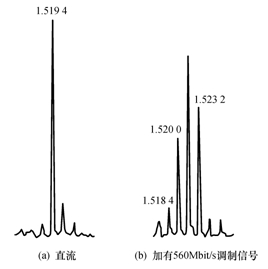 |
| 图4-32 普通激光器的静态和动态谱线 |
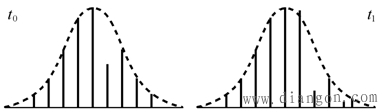 |
| 图4-33 高速调制时多纵模的随机起伏 |
| 4.啁啾声对中继距离的影响 模分配噪声的产生是由于激光器的多纵模性造成的,因而人们提出使用新型的单纵模激光器,以克服模分配噪声的影响,但随之又出现了新的问题. (l)啁啾声的产生 |
 |
|
对于处于直接强度调制状态下的单纵模激光器,其载流子密度的变化是随注入电流的变化而变化.这样使有源区的折射率指数发生变化,从而导致激光器谐振腔的光通路长度相应变化,结果致使振荡波长随时间偏移,这就是所谓的啁啾声现象. |
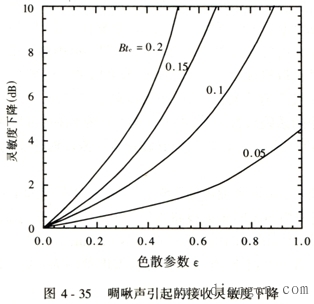 |
| 上述分析仅就啁啾声对接收灵敏度下降进行粗略的估算,实际上还有许多因素都致使啁啾声增加,导致接收灵敏度下降.例如当激光器的偏置处于阈值之上时,其啁啾声影响程度随之减小,但这会使消光比增加,如果消光比过大,同样会造成灵敏度下降,因而在实际系统设计中,存在最佳消光比,加之与系统中存在的啁啾声共同作用可使引起的灵敏度下降达到最小. 一般对于码速率为4 Gbit/s,传输距离IOO km的1.55μm光通信系统,若选用消光比10%左右的激光器,则系统的灵敏度下降达到最小值(2 dB).由于啁啾声的产生源于单纵模激光器在高速调制下,其载流子导致折射率变化,这样即使采用量子阱结构设计,也只能尽量减小这种折射率的变化,即减小啁啾声的影响,因而在较高速率的光纤通信系统中,都采用量子阱结构的DFB半导体激光器,若要彻底消除啁啾声的影响,则只能使系统工作于外调制状态,这样LD便工作于直流情况下. |
电工学习网 ( )
GMT+8, 2021-12-6 20:45