渐变型光纤光射线的理论分析

2015-3-24 08:32| 编辑:电工学习网| 查看: 22794| 评论: 0

    渐变型光纤的剖面折射指数分布已在图2-2（b）中给出。从图中可看出，渐变光纤芯子中的折射指数n1沿半径方向r是变化的，它随r的增加按一定规律减少，n1是r的函数，即为n1(r)，而包层中的折射指数n2一般是均匀的。
    下面将主要研究渐变型光纤中的子午线，以及用射线法分析如何在渐变型光纤中，得到最佳折射指数分布
    1．渐变型光纤中的子午线
    渐变型光纤中的射线，也分为子午线和斜射线两种。斜射线的情况比较复杂，因此对于渐变型光纤中的射线问题，只分析子午线，由此得出一些必要的公式和概念。
    如前所述，子午线是限制于光纤的子午面上。阶跃光纤的子午线，是经过轴线的直线；而渐变型光纤，由于芯子中的折射指数n1是随半径r变化的，因此子午线不是直线，而是曲线。它是靠折射原理将将子午线限制在芯子中沿轴线传输，如图2-8所示。由于芯子中的n1随r的增加而减少，因此在轴线处，折射指数最大，即n(0)=n1max；而在芯子和包层的交界面处，折射指数为n2，即n2=n1(a)。

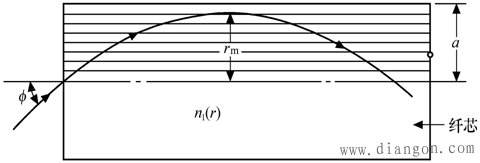图2-8 渐变型光纤中的子午线

    设入射点处r0=0，入射角为Φ，此时的法线为轴线。进入纤芯后的射线，由于折射指数n是从n1max→n2，因此光射线相当于是从光密媒质射向光疏媒质，此时法线垂直于轴线，则射线应离开法线而折射。当达到rm点后，射线几乎与轴线平行，而后又由光疏媒质射向光密媒质，射线又靠近法线而折射，这样形成了一条按周期变化的曲线。也就是不同入射条件的子午线，在芯子中，将有不同轨迹的折射曲线。
    2．子午线的轨迹方程
    由于渐变型光纤芯子中的折射指数n1随半径r变化，因此可将纤芯分成若干层折射指数不同的介质。在图2-9中，给出了渐变型光纤中的一个子午面，各层的折射指数为

而且

。
若一射线在光纤端面的r0点射入，射线的轴向角为θz0，则

，随着n(r)的减少，轴向角将逐渐减少，而相应的向各层介质入射光的入射角将逐渐增大，当射线到达rm点时

，这时

，在这一点，射线和轴线几乎平行。可以看出，射线轨迹与芯子中的折射率分布n(r)有关，也和射线的入射条件（n0、r0、θzo）有关。

图2-9子午线的行进轨迹

不管在哪层介质中，射线都应满足折射定律，利用折射定律，可推导如下关系：

    其中，n(r)——任一层介质的折射指数；
    θz——该层介质的轴向角。
    若令

，则可得

该式右端表示了射线的起始条件，它等于芯子中任一层介质的折射指数与轴向角余弦的乘积。
在图2-9中所表示的射线上，任取一点P，其轴向角为θz，ds为该点射线的切线，当ds→0时，

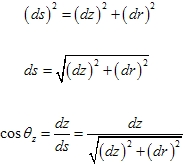利用式（2-27），则

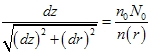经整理后，可得出

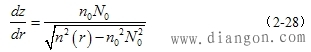也可写为

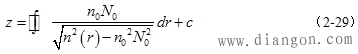    此式即为渐变型光纤子午线的轨迹方程。当光纤的折射指数分布n(r)和射线的起始条件n0,N0为已知时，即可利用式（2-29）求出r和z的关系，亦即可以定出射线的轨迹。
    3．渐变型光纤的最佳折射指数分布
    在渐变型光纤中，由于芯子中的折射指数分布不均匀，因此光射线的轨迹将不再是直线而是曲线。当射线的起始条件不同时，将有不同的轨迹存在。
    如果选用合适的n(r)分布，就有可能使芯子中的不同射线以同样的轴向速度前进，从而可减小光纤中的模式色散。关于光纤中的色散问题，将在后面详细讨论，这里只对其中模式色散作一简述描述。
    光功率以脉冲形式注入光纤后，将分布在光纤内所有模式之中，而不同模式沿着不同轨迹传输。每个模式的轴向传输速度不同，于是它们在相同的光纤长度上，到达某一点所需要的时间不同，从而使得沿光纤行进的脉冲在时间上展宽，这种色散称为模式色散。而渐变型光纤正是利用了n随变化r的特点，消除了模式色散。
    这种可以消除模式色散的n(r)分布，称为最佳折射指数分布。为了描述这个问题，将引入一个新的概念——自聚焦现象
    （1）光纤的自聚焦
    渐变型光纤中，不同射线具有相同轴向速度的现象称为自聚焦现象，这种光纤称为自聚焦光纤。
    前面已述，渐变型光纤芯子中的光射线，是周期变化的曲线，如图2-10 所示。射线①和射线②从A点到B点完成了一个周期的变化，轴线上的距离L称为空间周期长度。
    在渐变型光纤中，芯子轴线处（r=0）的折射指数最大，n随r的增加而逐渐减少。由于v=c/n，可以看出，靠近轴线处，射线的速度慢；远离轴线处，射线的速度快。当光纤中的射线传输相同的轴线长度时，则靠近轴线处的射线需要的时间长，但路程短；而远离轴线处的射线需要的时间短，但路程长。如果折射指数n的分布取得合适，则可使不同射线沿着不同轨迹在相同的时间内走完规定的轴线长度。也就是光纤中不同的子午线远离轴线的射线路径长，而靠近轴线的射线路径短，由于各点的光速不同，使它们在相同时间，具有相同的空间周期长度，即说明它们在光纤中可以自聚焦。

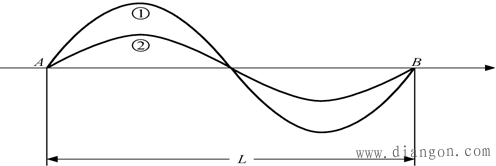图2-10 射线轨迹

    因此，不同的模式，在折射指数分布不均匀的光纤内，只要n(r)取得合适，可使它们沿着不同路径传输时，所需要的时间差别不是太大，即认为它们具有相同的轴向速度，从而消除了模式色散。
    这样，就得到一个结论：具有不同起始条件的子午线，如果它们的空间周期长度相同，则这些子午线将同时到达终端，就可以在光纤中产生自聚焦。这种可使光纤中产生自聚焦时的折射率分布，称为最佳折射指数分布。 
    （3）最佳折射指数分布的形式
    究竟什么样的折射指数分布形式，可以使得光纤内的子午线产生自聚焦呢？对于这个问题，必须是在一定的条件下来讨论，即
    ① 输入纤芯的光功率，对各个模式是均匀激励的；
    ② 光的中心波长λ0不变；
    ③ 各个模式在光纤中的传输损耗是相同的。
    根据前人经验，在这些假定条件下，当光纤芯子的折射率按双曲正割型分布时，不同起始条件的子午线，在纤芯中可得到相同的空间周期长度，即可以得到子午线的自聚焦。关于这个问题，应用渐变型光纤子午线的轨迹方程，即可得到证明。
    为了分析方便，常将光纤的折射指数分布函数，写成指数形式，即

    其中，n(0)——轴线处的折射指数；
    α——任意常数，也可称为渐变指数；
    A——与起始条件无关的常数。
    当 α=∞ 时，n(r)=n(0),即为阶跃光纤折射指数的表达式；
    当α为任意数时，代入式（2-30）中，则为渐变型光纤的折射指数表示式。这样，在α=2 时

称为平方律型光纤的折射指数表示式。它是渐变型光纤中的一种形式。
对于双曲正割型折射指数分布光纤，其折射指数分布可写为

它的幂级数展开式为

对于α=2的平方律型折射指数分布光纤，根据式（2-31），可写出它的展开式为

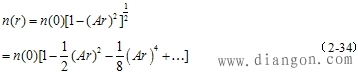如果忽略它们的高次项，则可以看出式（2-33）和式（2-34）有相同的形式，为

    因此，可得出这样的结论：
    严格来讲，只有折射指数按双曲正割型分布时的光纤，才可使光纤中子午线产生自聚焦。而由于平方律型折射指数分布光纤的折射率分布接近于双曲正割型光纤的折射率分布，因此可认为平方律型折射指数分布光纤具有较小的模式色散的特点。它的折射指数分布形式，接近于最佳折射指数分布，这样可简化分析。所以，在下面的讨论中，均以平方律型折射指数分布光纤为例。
    下面确定式（2-30）中的常数A.
    由式（2-30）可得出：

当r=a时，

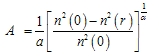因为

则得出

将式（2-38）代入式（2-30），得出

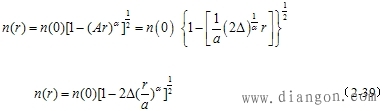此式为渐变型光纤α次方的折射率表示式。
当α=2时，得出

    式（2-40）即为平方律型折射指数分布光纤的折射指数表示式，亦称为渐变型光纤的最佳折射指数分布表示式。
    4．渐变型光纤的本地数值孔径
    在阶跃光纤中，由于芯子中的折射指数n1是不变的，因此，纤芯中各点的数值孔径都是相同的。而渐变型光纤芯子中折射指数n1是随半径r变化的，因此其数值孔径是芯子端面上位置的函数。所以把射入纤芯某点r处的光线的数值孔径，称为该点的本地数值孔径，记作NA(r)。只有当入射光线的端面入射角Φ<Φmax的射线，才可形成导波。
    对于渐变型光纤芯子中某一点的数值孔径，根据式（2-5），可写为

    式中，r为光纤芯子中任一点到轴线之间的距离；n(r)为该点的折射指数。
    从式（2-41）可看出，渐变型光纤的本地数值孔径与该点的折射指数n(r)有关。当折射指数越大时，本地数值孔径也越大，表示光纤捕捉射线的能力就越强。而芯子中的折射指数是随r的增加而减小的，轴线处的折射指数最大，即表明轴线处捕捉射线的能力最强。
    5. 平方律型折射指数分布光纤的模数量
    经推导（略）得平方律型折射指数分布光纤中总的模数量